Урок из серии «Геометрические алгоритмы»
Здравствуйте, дорогой читатель.
Решения многих задач вычислительной геометрии основывается на нахождении площади многоугольника. На этом уроке мы выведем формулу для вычисления площади многоугольника через координаты его вершин, напишем функцию для вычисления этой площади.
Задача. Вычислить площадь многоугольника, заданного координатами своих вершин, в порядке их обхода по часовой стрелке.
Сведения из вычислительной геометрии
Для вывода формулы площади многоугольника нам понадобятся сведения из вычислительной геометрии, а именно, понятие ориентированной площади треугольника.
Ориентированная площадь треугольника – это обычная площадь, снабженная знаком. Знак ориентированной площади треугольника АВС такой же, как у ориентированного угла между векторами и
. То есть ее знак зависит от порядка перечисления вершин.
Рис1
На рис. 1 треугольник АВС – прямоугольный. Его ориентированная площадь равна 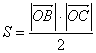
,
ориентирована положительно). Эту же величину можно вычислить другим способом.
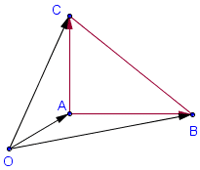
Пусть О – произвольная точка плоскости. На нашем рисунке площадь треугольника ABC получится, если из площади треугольника OBC вычесть площади OAB и OCA. Таким образом, нужно просто сложить ориентированные площади треугольников OAB, OBC и OCA. Это правило работает при любом выборе точки О.
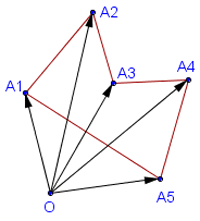
Точно так же для вычисления площади любого многоугольника нужно сложить ориентированные площади треугольников
Рис. 2
В сумме получится площадь многоугольника, взятая со знаком плюс, если при обходе ломаной многоугольника находится слева (обход границы против часовой стрелки), и со знаком минус, если он находится справа (обход по часовой стрелке).
Итак, вычисление площади многоугольника свелось к нахождению площади треугольника. Посмотрим, как выразить ее в координатах.
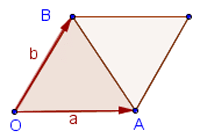
Векторное произведение двух векторов на плоскости есть площадь параллелограмма, построенного на этих векторах.
Векторное произведение, выраженное через координаты векторов:
Площадь треугольника будет равна половине этой площади:
В качестве точки О удобно взять начало координат, тогда координаты векторов, на основании которых вычисляются ориентированные площади, совпадут с координатами точек.
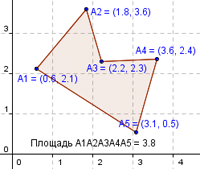
Пусть (х1, y1), (x2, у2), …, (хN,уN) —координаты вершин заданного многоугольника в порядке обхода по или против часовой стрелки. Тогда его ориентированная площадь S будет равна:
Это и есть наша рабочая формула, она используется в нашей программе.
Если координаты вершин были заданы в порядке обхода против часовой стрелки, то число S,вычисленное по этой формуле, получится положительным. В противном случае оно будет отрицательным, и для получения обычной геометрической площади нам необходимо взять его абсолютное значение.
Итак, рассмотрим программу для нахождения площади многоугольника, заданного координатами вершин.
Program geom6;
Const n_max=200; {максимальное количество точек+1}
type b=record
x,y:real;
end;
myArray= array[1..n_max] of b;
var input:text;
A:myArray;
s:real;
i,n:integer; procedure ZapMas(var n:integer; var A:myArray);
{Заполнение массива }
begin
assign(input,'input.pas');
reset(input);
readln(input, n);
for i:=1 to n do
read(input, a[i].x,a[i].y);
close(input);
end; function Square (A:myarray): real;
{Вычисление площади многоугольника}
var i:integer;
S: real;
begin
a[n+1].x:=a[1].x; a[n+1].y:=a[1].y;
s:=0;
for i:=1 to n do
s := s + (a[i].x*a[i+1].y - a[i].y*a[i+1].x);
s:=abs(s/2);
Square := S
end; {Square}
begin {main}
Zapmas(n, a);
PrintMas(a);
S:= Square(a);
writeln('S= ',s:6:2);
end. Координаты вершин считывается из файла input.pas., хранятся в массиве А в виде записей с двумя полями. Для удобства обхода многоугольника в массиве вводится n+1 элемент, значение которого равно значению первого элемента массива.
Входные данные:
5
0.6 2.1 1.8 3.6 2.2 2.3 3.6 2.4 3.1 0.5
Выходные данные:
S= 3.91
Мы решили задачу о нахождении площади многоугольника по координатам его вершин. Задачи усложняются. Если у вас есть замечания к этой статье, или пожелания, напишите в комментарии. Буду Вам очень признательна за сотрудничество.
До встречи на следующем уроке.
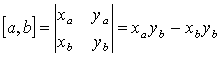
Спасибо! Очень хорошее объяснение формулы
Но я правильно понимаю, что данная точка О не должна совпадать с какой либо вершиной и должна лежать вне его.