Урок 31. Проверка принадлежности точки отрезку

Урок из серии «Геометрические алгоритмы»

Здравствуйте, дорогой читатель!

Сегодня мы рассмотрим еще одну типовую задачу из серии геометрические алгоритмы. Напишем функцию, которая будет проверять принадлежность произвольной точки отрезку, заданному координатами своего начала и конца.

Для реализации операций сравнения над вещественными данными напишем еще две функции: функцию EqPoint(), которая ,будет проверять, совпадают ли две точки на плоскости и функцию RealMoreEq() , которую будем использовать для проверки отношения «>=» (больше или равно).   Причина ввода специальных функций нам уже известна.

Решение.

Пусть точки — начальная и конечные точки отрезка. — произвольная точка на плоскости.

Вектор с началом в точке и концом в точке будет иметь координаты (x2-x1, y2-y1).

Если P(x, y) – произвольная точка, то координаты вектора равны: (x-x1, y – y1).

Точка Р будет принадлежать отрезку если:

1. Векторы в и коллинеарны (равно нулю их векторное произведение):
   , т.е. (x-x1)(y2-y1)-(y-y1)(x2-x1) = 0
2. Абсцисса точки P удовлетворяет условию: или . Иначе точка будет находиться на прямой левее или правее отрезка.

Program geom3;
Const _Eps: Real = 1e-3; {точность вычислений}
var x1,y1,x2,y2,x,y:real;
Function RealEq(Const a, b:Real):Boolean; {строго равно}
begin
  RealEq := Abs(a-b)<= _Eps
End; {RealEq}

Function RealMoreEq(Const a, b:Real):Boolean; {больше или равно}
begin
  RealMoreEq := a - b >= _Eps
End; {RealMoreEq}

Function EqPoint(x1,y1,x2,y2:real):Boolean;
{Совпадают ли две точки на плоскости}
begin
  EqPoint:=RealEq(x1,x2)and RealEq(y1,y2)
end; {EqPoint}
Function AtOtres(x1,y1,x2,y2,x,y:real):Boolean;
{Проверка принадлежности точки P отрезку P1P2}
Begin
  If EqPoint( x1,y1,x2,y2)
    Then  AtOtres:=  EqPoint( x1,y1,x,y)
    {точки P1 и P2 совпадают, результат определяется совпадением точек P1 и P}
Else
  AtOtres := RealEq((x-x1)*(y2-y1)- (y-y1)*(x2-x1),0)and (RealMoreEq(x,x1)and
    RealMoreEq( x2,x)Or RealMoreEq(x,x2)and RealMoreEq( x1,x))
end;  {AtOtres}

begin {main}
  writeln(Введите координаты точек: x1,y1,x2,y2,x,y');
  readln( x1,y1,x2,y2,x,y);
  if  AtOtres(x1,y1,x2,y2,x,y)
    then writeln('Да.')
    else writeln('Нет.);
end.  {main}

Результаты выполнения программы.

Результаты тестирования в программе GeoGebra:

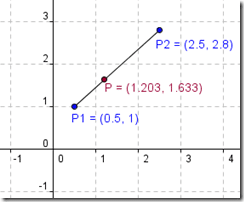
Сегодня мы написали функцию AtOtres() , которая проверяет принадлежность произвольной точки отрезку, заданному своими координатами.

Ввели еще две функции: EqPoint() и RealMoreEq() для реализации операций сравнения над вещественными данными. Первая проверяет, совпадают ли две точки на плоскости, вторая —  используется  для проверки отношения «>=».

На следующем уроке, на основе ранее написанных процедур, напишем процедуру определения координат точки пересечения двух отрезков.

На этом я с вами прощаюсь. До встречи на следующем уроке.