Урок 35. Построение выпуклой оболочки.

Урок из серии «Геометрические алгоритмы»

Вычисление выпуклой оболочки важно не только само по себе, но и как промежуточный этап для многих задач вычислительной геометрии.  Например, задача о наиболее удаленных точках.  Дано множество из  N точек. Нужно выбрать пару максимально удаленных друг от друга точек.

Выпуклой оболочкой конечного числа точек N называется наименьший, выпуклый многоугольник, содержащий все точки из N (некоторые из точек могут быть внутри многоугольника, некоторые на его сторонах, а некоторые будут его вершинами).

Наглядно это можно представить себе так: в точках N вбиваются гвозди, на которые натянута резинка, охватывающая их все – эта резинка и будет выпуклой оболочкой множества гвоздей.

Задача. На плоскости задано множество S точек. Найти вершины выпуклой оболочки этого множества.

Будем перечислять вершины в порядке обхода против часовой стрелки. Для эффективного решения этой задачи существует несколько различных алгоритмов. Приведем наиболее простую реализацию одного из них – алгоритма Джарвиса. Этот алгоритм иногда называют «заворачиванием подарка».

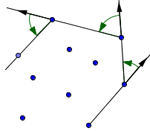
Перечисление точек искомой границы выпуклого многоугольника начнем с правой нижней точки ,  которая заведомо принадлежит границе выпуклой оболочки. Обозначим ее координаты .  Следующей при указанном порядке обхода будет точка . Она, очевидно, обладает тем свойством, что все остальные точки лежат слева от вектора , т.е. ориентированный угол между векторами и  неотрицателен для любой другой точки М нашего множества.

Для кандидата на роль точки проверяем выполнение условия со всеми точками М. Если точек, удовлетворяющих этому условию несколько, то вершиной искомого многоугольника станет та из них, для которой длина вектора максимальна.

Будем поступать так и далее.

Допустим, уже найдена i-я вершина выпуклой оболочки. Для следующей точки  косые произведения не отрицательны для всех точек М.

Если таких точек несколько, то выбираем ту, для которой вектор  имеет наибольшую длину.

Непосредственно поиск такой точки можно осуществить так. Сначала мы можем считать следующей (i+1)-й, любую точку.

Затем вычисляем значение , рассматривая в качестве М все остальные точки. Если для одной из них указанное выражение меньше нуля, то считаем следующей ее и продолжаем проверку остальных точек (аналогично алгоритму поиска минимального элемента в массиве).

Если же значение выражения равно нулю, то сравниваем квадраты длин векторов. Продолжая эту процедуру, мы рано или поздно вернемся к точке . Это будет означать, что выпуклая оболочка построена.

Приведем программу решения данной задачи для целочисленных координат.

Множество исходных точек находится в массиве a, а все точки, принадлежащие выпуклой оболочке, будем записывать в массив b.

program geom6;
type vv = record
       x,y: longint;
end;
    myArray = array[1..100] of vv;
var a, b: myArray;
    min,m,i,j,k,n:integer;
    input:text;
function vect(a1,a2,b1,b2:vv):longint;
  begin
    vect:=(a2.x - a1.x)*(b2.y-b1.y)-(b2.x-b1.x)*(a2.y-a1.y)
end;

function dist2(a1,a2:vv):longint; {Квадрат длины вектора}
begin
     dist2:=sqr(a2.x-a1.x)+sqr(a2.y-a1.y);
end;{dist2}

procedure Solve(a:myArray; var k: integer; var b:myArray);
{Построение выпуклой оболочки}
var i, j, m: integer;
begin
  {ищем правую нижнюю точку}
  m:=1;
  for i:= 2 to n do
    if a[i].y < a[m].y
      then m := i
       else if (a[i].y = a[m].y) and (a[i].x > a[m].x) then m:=i;
  {запишем ее в массив

 и переставим на первое место в массиве

}
  b[1] := a[m];   a[m]:= a[1];   a[1]:= b[1];
  k:= 1;
  min:= 2;

  writeln(b[1].x, b[1].y);
  repeat
    {ищем очередную вершину оболочки}
    for j := 2 to n do
      if (Vect(b[k],a[min],b[k],a[j])< 0) or
         ((Vect(b[k],a[min],b[k],a[j])=0) and
         (dist2(b[k],a[min])< dist2(b[k],a[j])))
        then min:=j;
    k:=k+1;
    {записана очередная вершина}
    b[k]:=a[min];
    min:=1;
  until (b[k].x = b[1].x)and (b[k].y = b[1].y); {пока ломаная не замкнется}
 end; {Solve}

begin{main}
  assign(input,'input.pas');
  reset(input);
  readln(input,n); {количество точек}
  for i:= 1 to n do
    read(input,a[i].x, a[i].y);
  close(input);
  solve(a, k, b);
  for j := 1 to k-1 do
    writeln(b[j].x, ' ',b[j].y)
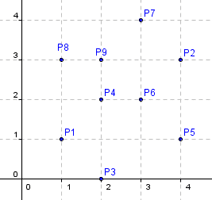
end.

Входные данные:
9
1 1 4 3 2 0 2 2 4 1 3 2 3 4 1 3 2 3

Выходные данные:
2 0 4 1 4 3 3 4 1 3 1 1

На этом мы с вами заканчиваем обзор решения элементарых задач вычислительной геометрии на плоскости. На них опирается решение более сложных , в частности олимпиадных задач.

Надеюсь, что решение последних окажется теперь нам по силам.

С уважением, Вера Господарец.