Урок из серии «Геометрические алгоритмы»
Здравствуйте, дорогой читатель. Напишем еще три новые функции.
Функция LinesCross() будет определять, пересекаются ли два отрезка. В ней взаимное расположение отрезков определяется с помощью векторных произведений. Для вычисления векторных произведений напишем функцию — VektorMulti().
Функция RealLess() будет использоваться для реализации операции сравнения «<» (строго меньше) для вещественных чисел.
Задача1. Два отрезка заданы своими координатами. Составить программу, которая определяет, пересекаются ли эти отрезки, не находя точку пересечения.
Решение
Пусть даны два отрезка. Первый задан точками . Второй задан точками
.
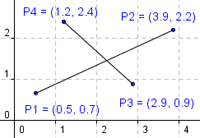
Взаимное расположение отрезков можно проверить с помощью векторных произведений:
Рассмотрим отрезок и точки
и
.
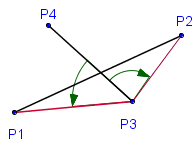
Точка расположена справа от прямой, для нее векторное произведение
< 0, так как векторы отрицательно ориентированы.
Для того чтобы точки и
, лежали по разные стороны от прямой
, достаточно, чтобы выполнялось условие
< 0 ( векторные произведения имели противоположные знаки).
Аналогичные рассуждения можно провести для отрезка и точек
и
.
Итак, если , то отрезки пересекаются.
Для проверки этого условия используется функцию LinesCross(), а для вычисления векторных произведений – функция VektorMulti().
Векторное произведение двух векторов вычисляется по формуле:
где:
ax, ay — координаты первого вектора,
bx, by — координаты второго вектора.
Program geometr4;
{Пересекаются ли 2 отрезка?}
Const _Eps: Real=1e-4; {точность вычслений}
var x1,y1,x2,y2,x3,y3,x4,y4: real;
var v1,v2,v3,v4: real; function RealLess(Const a, b: Real): Boolean; {Строго меньше}
begin
RealLess := b-a> _Eps
end; {RealLess} function VektorMulti(ax,ay,bx,by:real): real;
{ax,ay - координаты a
bx,by - координаты b }
begin
vektormulti:= ax*by-bx*ay;
end; Function LinesCross(x1,y1,x2,y2,x3,y3,x4,y4:real): boolean;
{Пересекаются ли отрезки?}
begin
v1:=vektormulti(x4-x3,y4-y3,x1-x3,y1-y3);
v2:=vektormulti(x4-x3,y4-y3,x2-x3,y2-y3);
v3:=vektormulti(x2-x1,y2-y1,x3-x1,y3-y1);
v4:=vektormulti(x2-x1,y2-y1,x4-x1,y4-y1);
if RealLess(v1*v2,0) and RealLess(v3*v4,0)
{v1v2<0 и v3v4<0, отрезки пересекаются}
then LinesCross:= true
else LinesCross:= false
end; {LinesCross} begin {main}
writeln('Введите координаты отрезков: x1,y1,x2,y2,x3,y3,x4,y4');
readln( x1,y1,x2,y2,x3,y3,x4,y4);
if LinesCross(x1,y1,x2,y2,x3,y3,x4,y4)
then writeln ('Да')
else writeln ('Нет')
end. Результаты выполнения программы:
Да.
Мы написали программу, определяющую, пересекаются ли отрезки, заданные своими координатами.
На следующем уроке мы составим алгоритм, с помощью которого можно будет определить, лежит ли точка внутри треугольника.
Уважаемый читатель. Вы уже познакомились с несколькими уроками из серии «Геометрические алгоритмы». Все ли доступно написано? Я буду Вам очень признательна, если Вы оставите отзыв об этих уроках. Возможно, что-то нужно еще доработать.
С уважением, Вера Господарец.
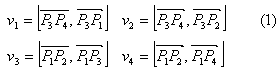
Сработает ли это, если ввести координаты -9 9 0 0 1 -1 2 -2 ? Это два отрезка на одной прямой, они не пересекаются, но, кажется, программа будет выдавать неверный ответ.
Да, они не пересекаются и программа дает верный ответ: «нет». Вы и сами можете это проверить. Но куда интереснее проверить, что выдает программа, если отрезки, лежащие на одной прямой а) касаются друг-друга (имеют одну общую точку) б) частично перекрываются в) совпадают. Итак:
а) -9 9 0 0 0 0 2 -2 Нет
б) -9 9 1 -1 0 0 2 -2 Нет
в) -9 9 2 -2 -9 9 2 -2 Нет
И если считать, что отрезки пересекаются в случае наличия у них ровно одной общей точки, программа работает верно для случаев частичного или полного перекрытия отрезков, но для случая, когда отрезки лежат на одной прямой и касаются друг-друга, ответ неверный. С другой стороны, касание не есть пересечение и тогда можно считать, про программа работает верно и в этом случае.
Прекрасно! Спасибо огромное!
Спасибо!!! Материал очень полезен и доступно изложен!!
Михаил, спасибо за подсказку. Исправила.
Класс! Вот как всё просто. Есть опечаточка где формула произведения (вместо «*» поставлен «-«)
Все хорошо написано
Cпасибо