Урок 33. Точка в многоугольнике

Урок из серии «Геометрические алгоритмы«

Здравствуйте, дорогой читатель! Продолжим знакомиться с геометрическими алгоритмами.

Полученный на прошлом уроке метод нахождения пересечения отрезков позволяет очень красиво решить задачу на принадлежность точки многоугольнику.

Задача. Даны точка P и простой N-угольник. Определить, принадлежит ли точка многоугольнику.

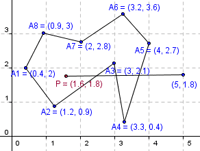
Пусть многоугольник на плоскости задается координатами своих N вершин в порядке обхода их по контуру по или против часовой стрелки (контур самопересечений не имеет). Для заданной точки P(x,y) определить, принадлежит ли она многоугольнику.

Идея решения этой задачи состоит в том, что нужно подсчитать количество пересечений луча, который имеет начало в данной точке P(x,y) и параллельного любой из осей координат. Для удобства возьмем ось абсцисс.

Из данного луча выделим отрезок с началом в точке P(x,y) и с концом в точке с максимальным значением абсциссы всех точек плюс 1 (эта точка заведомо находится вне многоугольника).

Далее подсчитываем количество пересечений данного отрезка со всеми сторонами многоугольника в порядке обхода их против или по  часовой стрелке. Если оно нечетное, то точка внутри, если четное — то снаружи. В алгоритме безразлично, выпуклый многоугольник  или нет.

Алгоритм решения этой задачи реализуется с помощью новой функции InsidePoint(). Кроме того в программе используются функции, написанные на прошлых уроках.

Итак, рассмотрим программу для определения принадлежности точки многоугольнику.

program geom5;
Const n=9; {Количество точек+1}
      _Eps: Real=1e-4; {точность вычислений}
type b=record
          x,y:real;
       end;
     myArray= array[1..n] of b;
var
    input:text;
    x,y:real;
    i:integer;
    a:myArray;

procedure zapmas;
begin
  assign(input,'input.pas');
  reset(input);
  for i:=1 to n-1 do
    read(input, a[i].x,a[i].y);
  readln(input, x,y);
  close(input);
end;

function RealLess(Const a, b: Real): Boolean; {строго меньше}
begin
  RealLess := b-a> _Eps
end; {RealLess}

function VektorMulti(ax,ay,bx,by:real): real;
{Векторное произведение векторов}
...
end;
Function LinesCross(x1,y1,x2,y2,x3,y3,x4,y4:real): boolean;
{Пересекаются ли отрезки?}
...
end;

function InsidePoint(a:myArray):Boolean;
{Проверка принадлежности точки многоугольнику}

var i,k,nom: integer;
    maxx:real;
begin
  k:=0;
  maxx:=a[1].x;
  nom:=1;
  for i:=2 to n-1 do
       if maxx < a[i].x then begin maxx:=a[i].x;nom:=i;end;
  a[n].x:=a[1].x;   a[n].y:=a[1].y;
  for i:=1 to n-1 do
    if LinesCross(a[i].x,a[i].y,a[i+1].x,a[i+1].y,x,y,a[nom].x+1,a[nom].y)
      then k:=k+1;
  if k mod 2 <> 0
    then  InsidePoint:= true
    else  InsidePoint:= false;
end;

begin {main}
  zapMas;
  if InsidePoint(a)
    then  writeln('Точка внутри многоугольника.')
    else  writeln('Точка вне многоугольнка.)
end.

Функции VektorMulti() (нахождения векторного произведения)  и LinesCross() ( определяющая, пересекаются ли отрезки), были рассмотрены  на прошлом уроке. Координаты многоугольника и заданной точки считываем из файла input.txt.

Предварительно находим для точек максимальное значение абсциссы x_max. Берем отрезок с началом в заданной точке P(x,y) и концом в точке с координамами (x_max+1, y). Далее подсчитываем количество пересечений этого отрезка со сторонами нашего многоугольника и делаем вывод о принадлежности точки многоугольнику.

Входные данные:
0.4 2 1.2 0.9 3 2.1 3.3 0.4 4 2.7 3.2 3.6 2 2.8 0.9 3
1.6 1.8
Выходные данные:
Точка внутри многоугольника.

Мы решили задачу определения принадлежности точки многоугольнику.

На этом я с Вами прощаюсь. До встречи на следующем уроке.