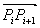Урок 30. Определение координат точки пересечения двух линий

Урок из серии «Геометрические алгоритмы»

Здравствуйте, дорогой читатель!

Продолжим знакомиться с геометрическими алгоритмами. На прошлом уроке мы нашли уравнение прямой линии по координатам двух точек. У нас получилось уравнение вида:

Сегодня мы напишем функцию, которая по уравнениям двух прямых линий будет находить координаты их точки пересечения (если такая имеется). Для проверки равенства вещественных чисел, будем использовать специальную функцию RealEq().

Точки на плоскости описываются парой вещественных чисел. При использовании вещественного типа операции сравнения лучше оформить специальными функциями.

Причина известна: на типе Real в системе программирования Паскаль нет отношения порядка, поэтому записи вида a = b, где a и b вещественные числа, лучше не использовать.
Сегодня мы введем в употребление функцию RealEq()  для реализации операции  «=» (строго равно) :

Function RealEq(Const a, b:Real):Boolean; {строго равно}
begin
  RealEq:=Abs(a-b)<=_Eps
End; {RealEq}

Задача. Заданы уравнения двух прямых: и . Найти точку их пересечения.

Решение. Очевидное решение состоит в том, чтобы решить систему уравнений прямых: 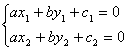Давайте перепишем эту системе несколько иначе:
(1)

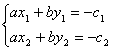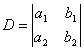
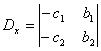
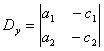
Введем обозначения: , , . Здесь D – определитель системы, а — определители, получающиеся в результате замены столбца коэффициентов при соответствующем неизвестном столбцом свободных членов. Если , то система (1) является определенной, то есть имеет единственное решение. Это решение можно найти по следующим формулам: , , которые называются формулами Крамера. Напомню, как вычисляется определитель второго порядка. В определителе различают две диагонали: главную и побочную. Главная диагональ состоит из элементов, взятых по направлению от верхнего левого угла определителя в нижний правый угол. Побочная диагональ – из правого верхнего в нижний левый. Определитель второго порядка равен произведению элементов главной диагонали минус произведение элементов побочной диагонали.

.

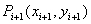
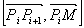
В программном коде для проверки проверка равенства  используется функция RealEq(). Вычисления над вещественными числами производятся с точностью до _Eps=1e-7.

program geom2;
Const _Eps: Real=1e-7;{точность вычислений}
var a1,b1,c1,a2,b2,c2,x,y,d,dx,dy:Real;

Function RealEq(Const a, b:Real):Boolean; {строго равно}
begin
  RealEq:=Abs(a-b)<=_Eps
End; {RealEq}

Function LineToPoint(a1,b1,c1,a2,b2,c2: real; var x,y:real):Boolean;
{Определение координат точки пересечения двух линий. Значение функции равно true,
если точка пересечения  есть,  и false, если прямые параллельны. }

var d:real;
begin
  d:=a1*b2-b1*a2;
  if Not(RealEq(d,0))

    then
      begin
        LineToPoint:=True;
        dx:=-c1*b2+b1*c2;
        dy:=-a1*c2+c1*a2;
        x:=dx/d;
        y:=dy/d;
      end
    else
      LineToPoint:=False
End;{LineToPoint}

begin {main}
  writeln('Введите коэффициенты уравнений: a1,b1,c1,a2,b2,c2 ');
  readln(a1,b1,c1,a2,b2,c2);

  if LineToPoint(a1,b1,c1,a2,b2,c2,x,y)
    then
      writeln(x:5:1,y:5:1)
    else
      writeln('Прямые параллельны.');
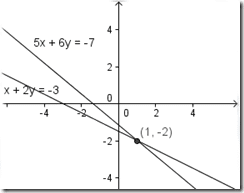
end.

Мы составили программу, с помощью которой можно, зная уравнения линий, найти координаты их точки пересечения.

Например, для линий, заданных уравнениями: x+2y+3 = 0 и 5x+6y+7=0 в результате получается точка с координатами: x= 1.0, y=-2.0.

На следующем уроке составим программу для определения принадлежности точки отрезку.

До встречи на следующем уроке.